支持向量机(四)-- 核函数
一、核函数的引入
问题1:
SVM显然是线性分类器,但数据如果根本就线性不可分怎么办?
解决方案1:
数据在原始空间(称为输入空间)线性不可分,但是映射到高维空间(称为特征空间)后很可能就线性可分了。
问题2:
映射到高维空间同时带来一个问题:在高维空间上求解一个带约束的优化问题显然比在低维空间上计算量要大得多,这就是所谓的“维数灾难”。
解决方案2:
于是就引入了“核函数”,核函数的价值在于它虽然也是讲特征进行从低维到高维的转换。
二、实例说明 例如图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
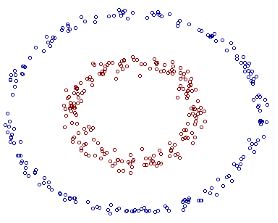
从上图我们可以看出一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,那么显然,上面的方程在新的坐标系下可以写作:
∑i=15aiZi+a6=0
关于新的坐标 Z ,这正是一个超平面 的方程!也就是说,如果我们做一个映射 ϕ:R2→R5 ,将 X 按照上面的规则映射为 Z ,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
三、详细分析
还记得之前我们用内积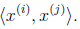 这里是二维模型,但是现在我们需要三维或者更高的维度来表示样本。这里我们假设是维度是三;
这里是二维模型,但是现在我们需要三维或者更高的维度来表示样本。这里我们假设是维度是三;
那么首先需要将特征x扩展到三维 ,然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射(feature mapping)。映射函数称作
,然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射(feature mapping)。映射函数称作 ,在这个例子中
,在这个例子中

我们希望将得到的特征映射后的特征应用于SVM分类,而不是最初的特征。这样,我们需要将前面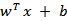 公式中的内积从
公式中的内积从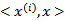 ,映射到
,映射到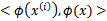 。
。
为什么需要映射后的特征而不是最初的特征来参与计算,一个重要原因是样例可能存在线性不可分的情况,而将特征映射到高维空间后,往往就可分了。
核函数的定义:
将核函数形式化定义,如果原始特征内积是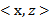 ,映射后为
,映射后为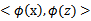 ,那么定义核函数(Kernel)为
,那么定义核函数(Kernel)为
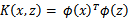
现在有了以上的概念,我们现在要计算K(x,z)只要简单的计算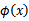 ,然后计算
,然后计算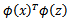 ,在求出它们的内积。但是现在有一个问题,那是计算K(x,z)的时间复杂度是提高了。即使是
,在求出它们的内积。但是现在有一个问题,那是计算K(x,z)的时间复杂度是提高了。即使是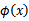 计算也是很复杂的。那现在怎么解决呢?
计算也是很复杂的。那现在怎么解决呢?
现在我们假设:x,z都是n维,同时有
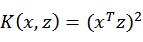
展开
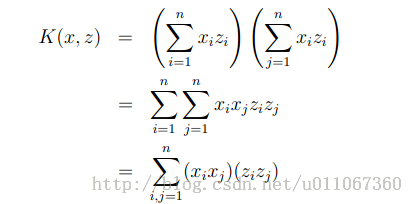
发现我们可以只计算原始特征x和z内积的平方(时间复杂度是O(n)),就等价与计算映射后特征的内积。也就是说我们不需要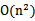 时间了。
时间了。
现在看一下映射函数(n=3时),根据上面的公式,得到
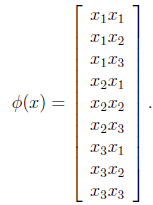
也就是说核函数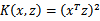 只能在选择这样的
只能在选择这样的 作为映射函数时才能够等价于映射后特征的内积。
作为映射函数时才能够等价于映射后特征的内积。
再看一个核函数

对应的映射函数(n=3时)是
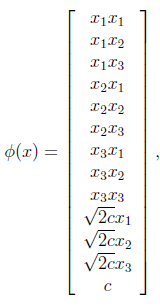
更一般地,核函数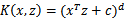 对应的映射后特征维度为
对应的映射后特征维度为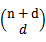 。
。
四、如何映射到核函数
现在介绍了核函数之后那到底怎么来使用核函数到样本了?
设超平面实际的方程是这个样子(圆心在 X2 轴上的一个正圆):
a1X21+a2(X2−c)2+a3=0
因此我只需要把它映射到 Z1=X21, Z2=X22, Z3=X2 这样一个三维空间中即可,下图是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:
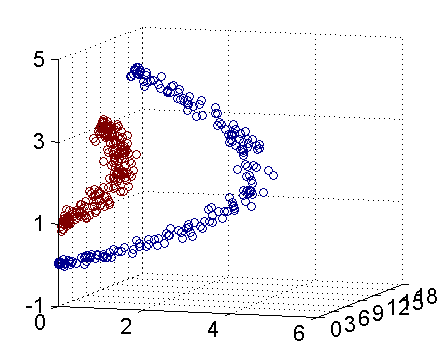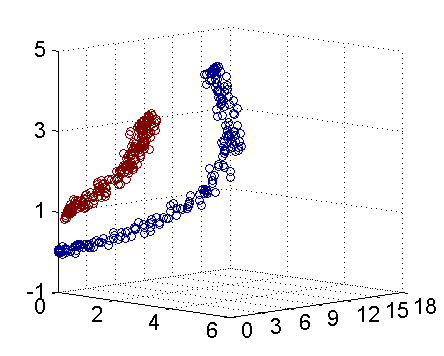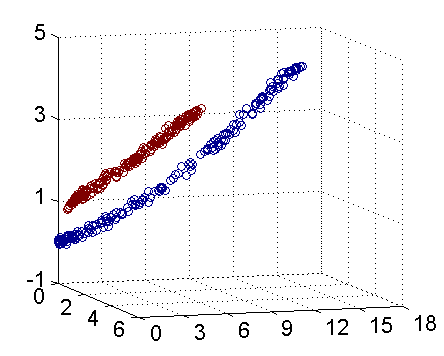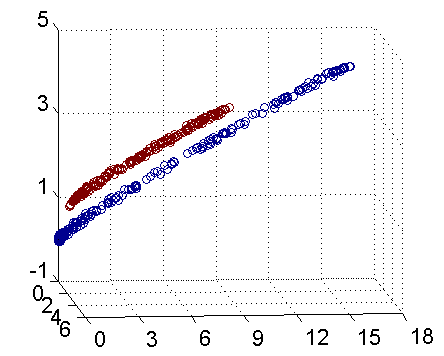
现在让我们再回到 SVM 的情形,假设原始的数据时非线性的,我们通过一个映射 ϕ(⋅) 将其映射到一个高维空间中,数据变得线性可分了,这个时候,我们就可以使用原来的推导来进行计算,只是所有的推导现在是在新的空间,而不是原始空间中进行。
我们上一次得到的最终的分类函数是这样的:

现在则是在映射过后的空间,即:
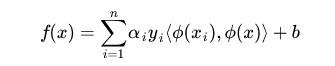
而其中的 α 也是通过求解如下 dual 问题而得到的:
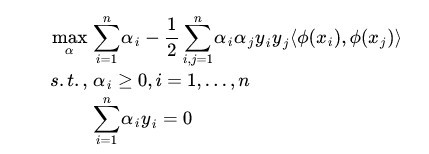
回到我们之前构造的一个五维的空间:到现在貌似我们还没有用到核函数,但是现在我们可以看出,数据映射到新空间后,因为新空间是多维的,计算量肯定是增加了不少了,现在就只能用核函数来解决了。
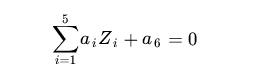
不妨还是从最开始的简单例子出发,设两个向量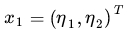 和
和  ,而ϕ(*) 即是到前面说的五维空间的映射,
,而ϕ(*) 即是到前面说的五维空间的映射,
五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,
因此映射过后的内积为:
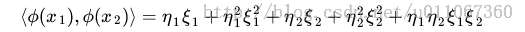
根据我们之前简介的核函数的实现,具体来说,上面这个式子的计算结果实际上映射了
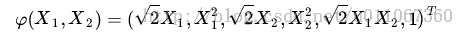
这样一来计算的问题就算解决了,避开了直接在高维空间中进行计算,而结果却是等价的。
五、高斯核函数
再看另外一个核函数
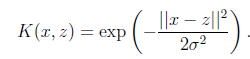
这时,如果x和z很相近( ),那么核函数值为1,如果x和z相差很大(
),那么核函数值为1,如果x和z相差很大(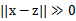 ),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
既然高斯核函数能够比较x和z的相似度,并映射到0到1,回想logistic回归,sigmoid函数可以,因此还有sigmoid核函数等等。
注意,使用核函数后,怎么分类新来的样本呢?线性的时候我们使用SVM学习出w和b,新来样本x的话,我们使用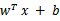 来判断,如果值大于等于1,那么是正类,小于等于是负类。在两者之间,认为无法确定。如果使用了核函数后,
来判断,如果值大于等于1,那么是正类,小于等于是负类。在两者之间,认为无法确定。如果使用了核函数后,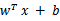 就变成了
就变成了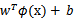 ,是否先要找到
,是否先要找到 ,然后再预测?答案肯定不是了,找
,然后再预测?答案肯定不是了,找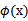 很麻烦,回想我们之前说过的
很麻烦,回想我们之前说过的
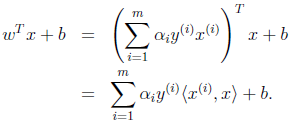
只需将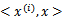 替换成
替换成 ,然后值的判断同上。
,然后值的判断同上。
总结:对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(*) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了 SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。
参考文档:( 主要的参考文档来自4个地方)
4、斯坦福大学机器学习的公开课。